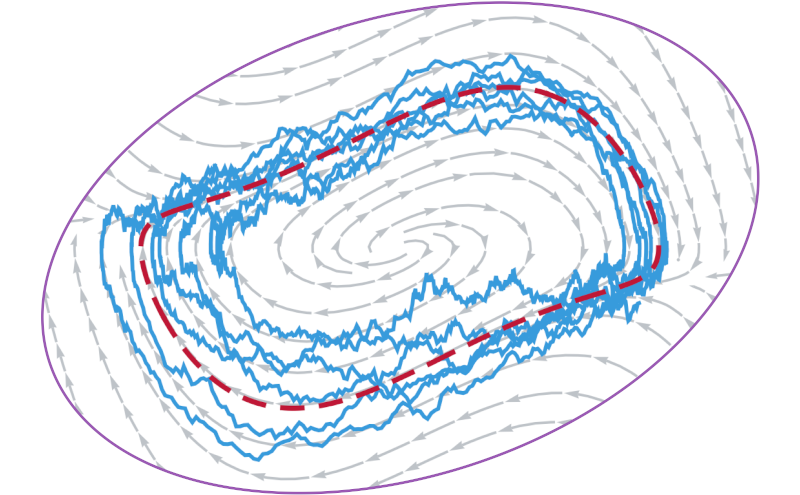
How to construct a simple linear model for Van der Pol relaxation oscillations? Learn about it in our new paper and see how it applies to hair cells’ bundle oscillations!
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.102.032209
Volterra-series approach to stochastic nonlinear dynamics: Linear response of the Van der Pol oscillator driven by white noise
Roman Belousov1 (@ribelousov), Florian Berger2 (@DrFlorianBerger), and A. J. Hudspeth.2
1 The Abdus Salam International Centre for Theoretical Physics (@ictpnews)
2 The Rockefeller University (@RockefellerUniv)
The Van der Pol equation is a paradigmatic nonlinear model of self-sustained oscillatory motion that describes various rhythmic processes in physics and biology, such as the active oscillations of mechanoreceptive hair bundles in the hearing organs of vertebrates. The nontrivial statistics of such oscillations is often influenced by the ubiquitous environmental noise in real systems, whose complex behavior can be analyzed with help of a novel theoretical approach based on Volterra series. As demonstrated in the present article, this mathematical technique allows us to estimate the system’s parameter values directly from experimental time series.