Now it is time to say my thanks to all my colleagues at ICTP and @edgarroldankb’s lab for the science and fun—we had that a lot despite of the pandemic 2020—and “Hello!” to @ErzbergerGroup at EMBL!

Now it is time to say my thanks to all my colleagues at ICTP and @edgarroldankb’s lab for the science and fun—we had that a lot despite of the pandemic 2020—and “Hello!” to @ErzbergerGroup at EMBL!
In the background of virtual teaching and conferencing, our story on the first-passage fingerprints of diffusive dynamics has been featured on the back cover of Soft Matter 16, 2020.

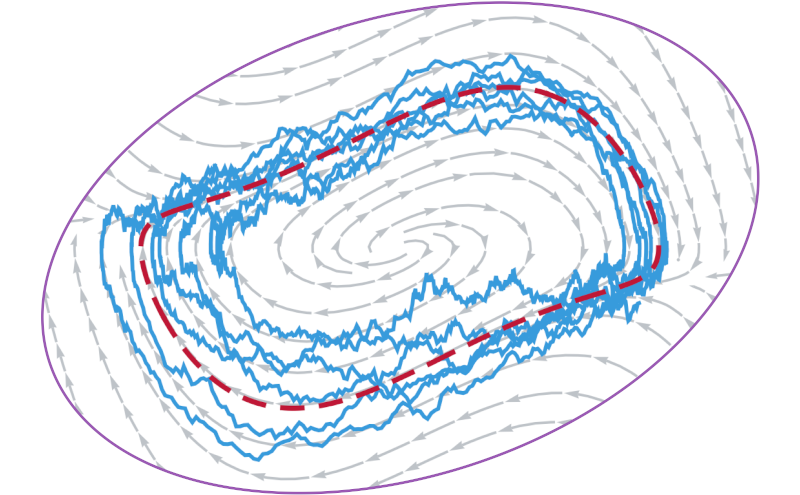

How to construct a simple linear model for Van der Pol relaxation oscillations? Learn about it in our new paper and see how it applies to hair cells’ bundle oscillations!
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.102.032209
Roman Belousov1 (@ribelousov), Florian Berger2 (@DrFlorianBerger), and A. J. Hudspeth.2
1 The Abdus Salam International Centre for Theoretical Physics (@ictpnews)
2 The Rockefeller University (@RockefellerUniv)
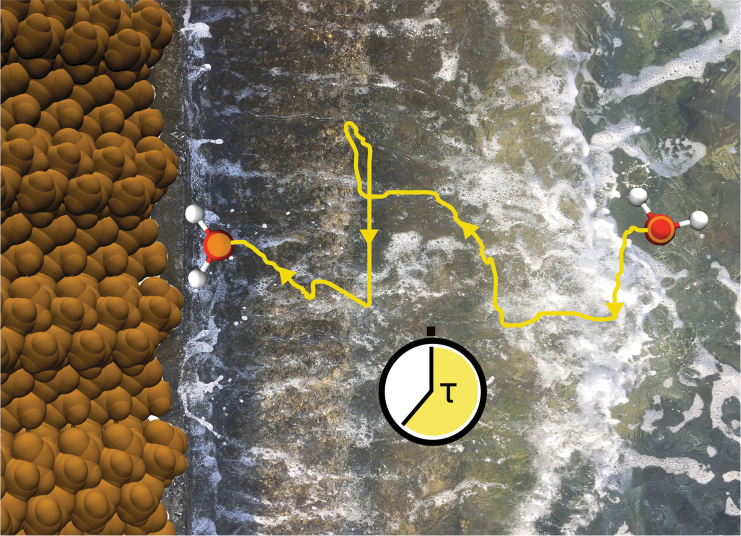
Check out an exciting story of our lab’s (@edgarroldankb) new collaboration with Hassanali’s group on first-passage time fingerprints of molecules’ diffusive dynamics!
Roman Belousov (@ribelousov), Muhammad Nawaz Qaisrani, Ali Hassanali, Édgar Roldán (@edgarroldankb) — ICTP (@ictpnews)
https://arxiv.org/abs/2003.12615
▸ More
Couple of new publications that have gone online during this summer: a preprint on Volterra-series approach to the Van der Pol oscillator driven by white noise, and a presentation on higher-order memory and inertia effects in the Onsager-Machlup fluctuation theory.

– R. Belousov, F. Berger, A.J. Hudspeth
http://arxiv.org/abs/1908.05313
The Van der Pol equation is a paradigmatic model of relaxation oscillations. This remarkable nonlinear phenomenon of self-sustained oscillatory motion underlies important rhythmic processes in nature and electrical engineering. Relaxation oscillations in a real system are usually coupled to environmental noise, which further complicates their dynamics. Determination of the equation parameter values becomes then a difficult task. In a companion paper we have proposed an analytical approach to a similar problem for another classical nonlinear model—the bistable Duffing oscillator. Here we extend our techniques to the case of the Van der Pol equation driven by white noise. We analyze the statistics of solutions and propose a method to estimate parameter values from the oscillator’s time series.
– R. Belousov, E. Roldan
▸ More

May 10, 2019 at 17.30 come to attend our contributed talk at Nordita in Stockholm!
– Roman Belousov (@ribelousov), Florian Berger (@DrFlorianBerger), A. J. Hudspeth.

Roman Belousov (@ribelousov), Florian Berger (@DrFlorianBerger), A. J. Hudspeth.
▸ More